8 основных структур данных в Python ������������-�������������� target=

Что такое структуры данных?

Структуры данных — это структуры кода для хранения и организации данных, которые упрощают изменение, навигацию и доступ к информации. Структуры данных определяют способ сбора данных, функциональные возможности, которые мы можем реализовать, и отношения между данными.

Структуры данных используются практически во всех областях информатики и программирования, от операционных систем до интерфейсной разработки и машинного обучения.

Структуры данных помогают:

• Управляйте большими наборами данных и используйте их.
• Быстрый поиск определённых данных в базе данных.
• Создавайте чёткие иерархические или реляционные связи между точками данных.
• Упростите и ускорьте обработку данных.

Структуры данных являются жизненно важными строительными блоками для эффективного решения реальных проблем. Структуры данных — это проверенные и оптимизированные инструменты, которые дают вам удобную основу для организации ваших программ. В конце концов, вам не нужно переделывать колесо (или конструкцию) каждый раз, когда это нужно.

У каждой структуры данных есть задача или ситуация, для решения которой она наиболее подходит. Python имеет 4 встроенных структуры данных, списки, словари, кортежи и наборы. Эти встроенные структуры данных поставляются с методами по умолчанию и негласной оптимизацией, которая упрощает их использование.

Большинство структур данных в Python являются их модифицированными формами или используют встроенные структуры в качестве основы.

• Список: структуры, похожие на массивы, которые позволяют сохранять набор изменяемых объектов одного и того же типа в переменную.
• Кортеж: кортежи — это неизменяемые списки, то есть элементы не могут быть изменены. Он объявлен в круглых скобках вместо квадратных.
• Набор: наборы — это неупорядоченные коллекции, что означает, что элементы неиндексированы и не имеют установленной последовательности. Они объявляются фигурными скобками.
• Словарь (dict): Подобно хэш-карте или хеш-таблицам на других языках, словарь представляет собой набор пар ключ / значение. Вы инициализируете пустой словарь пустыми фигурными скобками и заполняете его ключами и значениями, разделёнными двоеточиями. Все ключи — уникальные неизменяемые объекты.

Теперь давайте посмотрим, как мы можем использовать эти структуры для создания всех сложных структур, которые ищут интервьюеры.

Массивы (списки) в Python

Python не имеет встроенного типа массива, но вы можете использовать списки для всех тех же задач. Массив — это набор значений одного типа, сохранённых под тем же именем.

Каждое значение в массиве называется «элементом», и индексирование соответствует его положению. Вы можете получить доступ к определённым элементам, вызвав имя массива с индексом желаемого элемента. Вы также можете получить длину массива с помощью len()метода.

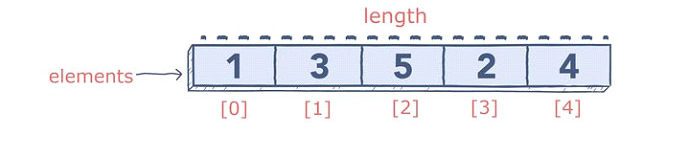
В отличие от языков программирования, таких как Java, которые имеют статические массивы после объявления, массивы Python автоматически увеличиваются или уменьшаются при добавлении / вычитании элементов.

Например, мы могли бы использовать этот append()метод для добавления дополнительного элемента в конец существующего массива вместо объявления нового массива.

Это делает массивы Python особенно простыми в использовании и адаптируемыми на лету.

cars = [«Toyota», «Tesla», «Hyundai»]

print(len(cars))

cars.append(«Honda»)

cars.pop(1)

for x in cars:

  print(x)

Преимущества:

• Простота создания и использования последовательностей данных.
• Автоматическое масштабирование в соответствии с меняющимися требованиями к размеру.
• Используется для создания более сложных структур данных.

Недостатки:

• Не оптимизирован для научных данных (в отличие от массива NumPy).
• Может управлять только крайним правым концом списка.

Приложения:

• Совместное хранилище связанных значений или объектов, т.е. myDogs.
• Коллекции данных, которые вы будете просматривать.
• Коллекции структур данных, например, список кортежей.

Общие вопросы собеседования с массивами в Python

• Удалить чётные числа из списка.
• Объединить два отсортированных списка.
• Найдите минимальное значение в списке.
• Подсписок максимальной суммы.
• Печать продукции всех элементов.

 

Очереди в Python

Очереди — это линейная структура данных, в которой данные хранятся в порядке «первым пришёл — первым ушёл» (FIFO). В отличие от массивов, вы не можете получить доступ к элементам по индексу, а вместо этого можете извлечь только следующий самый старый элемент. Это делает его отличным решением для задач, чувствительных к заказу, таких как обработка онлайн-заказов или хранение голосовой почты.

Вы можете представить очередь как очередь в продуктовом магазине; кассир не выбирает, кого проверять следующим, а скорее обрабатывает человека, который дольше всех стоял в очереди.

Мы могли бы использовать список Python с append() и pop() методами для реализации очереди. Однако это неэффективно, потому что списки должны сдвигать все элементы на один индекс всякий раз, когда вы добавляете новый элемент в начало.

Вместо этого лучше всего использовать deque класс из collections модуля Python. Deques оптимизированы для операций добавления и извлечения. Deque реализация также позволяет создавать двухсторонние очереди, которые могут получить доступ к обеим сторонам очередей через popleft() и popright() методы.

from collections import deque

# Initializing a queue

q = deque()

# Adding elements to a queue

q.append(‘a’)

q.append(‘b’)

q.append(‘c’)

print(«Initial queue»)

print(q)

# Removing elements from a queue

print(«\nElements dequeued from the queue»)

print(q.popleft())

print(q.popleft())

print(q.popleft())

print(«\nQueue after removing elements»)

print(q)

# Uncommenting q.popleft()

# will raise an IndexError

# as queue is now empty

Преимущества:

• Автоматически упорядочивает данные в хронологическом порядке.
• Весы в соответствии с требованиями к размеру.
• Эффективное время с dequeклассом.

Недостатки:

• Доступ к данным возможен только на концах.

Приложения:

• Операции с общим ресурсом, таким как принтер или ядро ЦП.
• Служит временным хранилищем для пакетных систем.
• Обеспечивает простой порядок по умолчанию для задач равной важности.

Общие вопросы на собеседовании в очереди на Python

• Обратить первые k элементов очереди.
• Реализуйте очередь, используя связанный список.
• Реализуйте стек с помощью очереди.

Стеки в Python

Стеки представляют собой последовательную структуру данных, которая действует как версия очередей «последний пришёл — первым ушёл» (LIFO). Последний элемент, вставленный в стек, считается верхним в стеке и является единственным доступным элементом. Чтобы получить доступ к среднему элементу, вы должны сначала удалить достаточное количество элементов, чтобы нужный элемент находился на вершине стека.

Многие разработчики представляют стопки как стопку обеденных тарелок; вы можете добавлять или убирать тарелки в верхнюю часть стопки, но вам нужно переместить всю стопку, чтобы разместить одну внизу.

Добавление элементов называется выталкиванием, а удаление элементов — всплывающим сообщением. Вы можете реализовать стеки в Python, используя встроенную структуру списка. При реализации списка в операциях push используется append()метод, а в операциях pop — pop().

stack = []

# append() function to push

# element in the stack

stack.append(‘a’)

stack.append(‘b’)

stack.append(‘c’)

print(‘Initial stack’)

print(stack)

# pop() function to pop

# element from stack in

# LIFO order

print(‘\nElements popped from stack:’)

print(stack.pop())

print(stack.pop())

print(stack.pop())

print(‘\nStack after elements are popped:’)

print(stack)

# uncommenting print(stack.pop())

# will cause an IndexError

# as the stack is now empty

Преимущества:

• Предлагает управление данными LIFO, которое невозможно с массивами.
• Автоматическое масштабирование и очистка объекта.
• Простая и надёжная система хранения данных.

Недостатки:

• Память стека ограничена.
• Слишком много объектов в стеке приводит к ошибке переполнения стека.

Приложения:

• Используется для создания высокореактивных систем.
• Системы управления памятью используют стеки для обработки в первую очередь самых последних запросов.
• Полезно для таких вопросов, как сопоставление скобок.

Общие вопросы собеседования по стекам в Python

• Реализуйте очередь, используя стеки.
• Вычислить выражение Postfix с помощью стека.
• Следующий по величине элемент, использующий стек.
• Создать min() функцию с использованием стека.

Связанные списки в Python

Связанные списки — это последовательный набор данных, который использует реляционные указатели на каждом узле данных для связи со следующим узлом в списке.

В отличие от массивов, связанные списки не имеют объективных позиций в списке. Вместо этого у них есть относительные позиции, основанные на их окружающих узлах.

Первый узел в связанном списке называется головным узлом, а последний — хвостовым узлом, который имеет nullуказатель.

Связанные списки могут быть односвязными или дважды связанными в зависимости от того, имеет ли каждый узел только один указатель на следующий узел или он также имеет второй указатель на предыдущий узел.

Вы можете думать о связанных списках как о цепочке; отдельные ссылки имеют связь только со своими ближайшими соседями, но все ссылки вместе образуют более крупную структуру.

Python не имеет встроенной реализации связанных списков и поэтому требует, чтобы вы реализовали Nodeкласс для хранения значения данных и одного или нескольких указателей.

Связанные списки в основном используются для создания расширенных структур данных, таких как графики и деревья, или для задач, требующих частого добавления / удаления элементов по всей структуре.

Преимущества:

• Эффективная вставка и удаление новых элементов.
• Проще реорганизовать, чем массивы.
• Полезно в качестве отправной точки для сложных структур данных, таких как графики или деревья.

Недостатки:

• Хранение указателей с каждой точкой данных увеличивает использование памяти.
• Всегда должен перемещаться по связанному списку от узла Head, чтобы найти определённый элемент.

Приложения:

• Строительный блок для расширенных структур данных.
• Решения, требующие частого добавления и удаления данных.

Общие вопросы собеседования по связному списку в Python

• Распечатать средний элемент данного связанного списка.
• Удалить повторяющиеся элементы из отсортированного связного списка.
• Проверьте, является ли односвязный список палиндромом.
• Объединить K отсортированных связанных списков.
• Найдите точку пересечения двух связанных списков.

Циркулярно связанные списки в Python

Основным недостатком стандартного связного списка является то, что вам всегда нужно начинать с узла Head.

Циклический связанный список устраняет эту проблему, заменяя nullуказатель узла Tail указателем на узел Head. При обходе программа будет следовать указателям, пока не достигнет узла, на котором она была запущена.

Преимущество этой настройки заключается в том, что вы можете начать с любого узла и пройти по всему списку. Это также позволяет вам использовать связанные списки в качестве зацикленной структуры, задав желаемое количество циклов через структуру.

Списки с круговой связью отлично подходят для процессов, которые зацикливаются в течение длительного времени, например, распределение ЦП в операционных системах.

Преимущества:

• Может просматривать весь список, начиная с любого узла.
• Делает связанные списки более подходящими для циклических структур.

Недостатки:

• Сложнее найти узлы Head и Tail списка без nullмаркера.

Приложения:

• Регулярно зацикливающиеся решения, такие как планирование ЦП.
• Решения, в которых вам нужна свобода начать обход с любого узла.

Общие вопросы собеседования со связным списком в Python

• Обнаружить петлю в связанных списках.
• Перевернуть круговой связанный список.
• Обратный круговой связанный список в группах заданного размера.

Деревья в Python

Деревья — это ещё одна основанная на отношениях структура данных, которая специализируется на представлении иерархических структур. Как и связанный список, они заполняются Nodeобъектами, которые содержат значение данных и один или несколько указателей для определения его отношения к непосредственным узлам.

Каждое дерево имеет корневой узел, от которого отходят все остальные узлы. Корень содержит указатели на все элементы непосредственно под ним, которые известны как его дочерние узлы. Эти дочерние узлы могут иметь собственные дочерние узлы. У двоичных деревьев не может быть узлов с более чем двумя дочерними узлами.

Любые узлы на одном уровне называются одноуровневыми узлами. Узлы без подключённых дочерних узлов называются листовыми узлами.

Наиболее распространённое применение двоичного дерева — это двоичное дерево поиска. Деревья двоичного поиска превосходно подходят для поиска больших наборов данных, поскольку временная сложность зависит от глубины дерева, а не от количества узлов.

Деревья двоичного поиска имеют четыре строгих правила:

• Левое поддерево содержит только узлы с элементами меньше корня.
• Правое поддерево содержит только узлы с элементами больше корня.
• Левое и правое поддеревья также должны быть двоичным деревом поиска. Они должны следовать приведённым выше правилам с «корнем» своего дерева.
• Не может быть повторяющихся узлов, т.е. никакие два узла не могут иметь одинаковое значение.

class Node:

    def __init__(self, data):

        self.left = None

        self.right = None

        self.data = data

    def insert(self, data):

# Compare the new value with the parent node

        if self.data:

            if data < self.data:

                if self.left is None:

                    self.left = Node(data)

                else:

                    self.left.insert(data)

            elif data > self.data:

                if self.right is None:

                    self.right = Node(data)

                else:

                    self.right.insert(data)

        else:

            self.data = data

# Print the tree

    def PrintTree(self):

        if self.left:

            self.left.PrintTree()

        print( self.data),

        if self.right:

            self.right.PrintTree()

# Use the insert method to add nodes

root = Node(12)

root.insert(6)

root.insert(14)

root.insert(3)

root.PrintTree()

Преимущества:

• Подходит для представления иерархических отношений.
• Динамический размер, отличный масштаб.
• Операции быстрой вставки и удаления.
• В двоичном дереве поиска вставленные узлы сразу же упорядочиваются..
• Деревья двоичного поиска эффективны при поиске; длина только O (высота).

Недостатки:

• Время дорогое, O (войти) 4O ( l o g n ) 4, чтобы изменить или «сбалансировать» деревья или извлечь элементы из известного местоположения.
• Дочерние узлы не содержат информации о своих родительских узлах, и их трудно перемещать назад.
• Работает только для отсортированных списков. Несортированные данные превращаются в линейный поиск.

Приложения:

• Отлично подходит для хранения иерархических данных, таких как расположение файла.
• Используется для реализации лучших алгоритмов поиска и сортировки, таких как двоичные деревья поиска и двоичные кучи.

Общие вопросы на собеседовании с деревом в Python

• Проверьте, идентичны ли два двоичных дерева.
• Реализовать обход порядка уровней бинарного дерева.
• Распечатайте периметр двоичного дерева поиска.
• Суммируйте все узлы на пути.
• Подключите всех братьев и сестёр двоичного дерева.

Графы в Python

Графы — это структура данных, используемая для визуального представления взаимосвязей между вершинами данных (узлами графа). Связи, соединяющие вершины вместе, называются рёбрами.

Рёбра определяют, какие вершины соединяются, но не указывают направление потока между ними. Каждая вершина имеет соединения с другими вершинами, которые сохраняются в вершине в виде списка, разделённого запятыми.

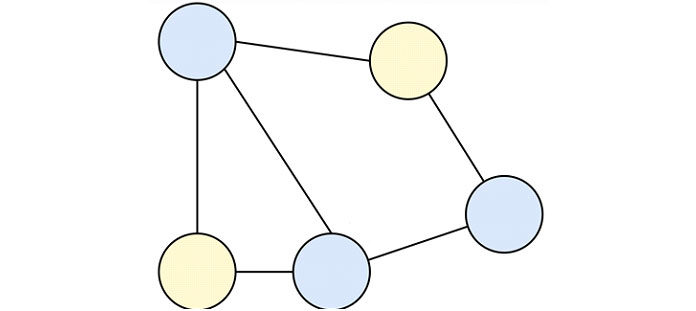
Undirected

Существуют также специальные графы, называемые ориентированными графами, которые определяют направление взаимосвязи, аналогично связному списку. Направленные графы полезны при моделировании односторонних отношений или структур, подобных блок-схемам.

Directed

Они в основном используются для передачи визуальных сетей веб-структур в кодовой форме. Эти структуры могут моделировать множество различных типов отношений, таких как иерархии, ветвящиеся структуры или просто быть неупорядоченной реляционной сетью. Универсальность и интуитивность графиков делают их фаворитом в науке о данных.

При написании в виде обычного текста графы имеют список вершин и рёбер:

V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}

В Python графы лучше всего реализовать с использованием словаря с именем каждой вершины в качестве ключа и списком рёбер в качестве значений.

# Create the dictionary with graph elements

graph = { «a» : [«b»,»c»],

                 «b» : [«a», «d»],

                 «c» : [«a», «d»],

                  «d» : [«e»],

                  «e» : [«d»]

         }

# Print the graph

print(graph)

Преимущества:

• Быстро передавайте визуальную информацию с помощью кода.
• Подходит для моделирования широкого спектра реальных проблем.
• Простой в освоении синтаксис.

Недостатки:

• Связи вершин трудно понять в больших графах.
• Дорогое время для анализа данных с графика.

Приложения:

• Отлично подходит для моделирования сетей или веб-структур.
• Используется для моделирования сайтов социальных сетей, таких как Facebook.

Общие вопросы собеседования с графиком в Python

• Обнаружить цикл в ориентированном графе.
• Найдите «материнскую вершину» в ориентированном графе.
• Подсчитать количество рёбер в неориентированном графе.
• Проверить, существует ли путь между двумя вершинами.
• Найдите кратчайший путь между двумя вершинами.

Хеш-таблицы в Python

Хеш-таблицы — это сложная структура данных, способная хранить большие объёмы информации и эффективно извлекать определённые элементы.

В этой структуре данных используются пары ключ / значение, где ключ — это имя желаемого элемента, а значение — это данные, хранящиеся под этим именем.

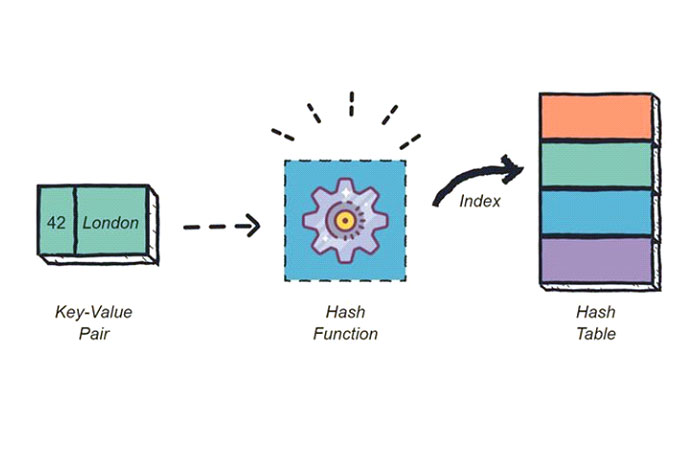
Каждый входной ключ проходит через хеш-функцию, которая преобразует его из начальной формы в целочисленное значение, называемое хешем. Хеш-функции всегда должны генерировать один и тот же хэш из одного и того же ввода, должны быстро вычислять и выдавать значения фиксированной длины. Python включает встроенную hash()функцию, ускоряющую реализацию.

Затем таблица использует хеш-код для нахождения общего местоположения желаемого значения, называемого корзиной хранения. После этого программе нужно будет искать нужное значение только в этой подгруппе, а не во всём пуле данных.

Помимо этой общей структуры, хеш-таблицы могут сильно отличаться в зависимости от приложения. Некоторые могут разрешать ключи из разных типов данных, в то время как некоторые могут иметь разные настройки сегментов или разные хеш-функции.

Вот пример хеш-таблицы в коде Python:

import pprint

class Hashtable:

    def __init__(self, elements):

        self.bucket_size = len(elements)

        self.buckets = [[] for i in range(self.bucket_size)]

        self._assign_buckets(elements)

    def _assign_buckets(self, elements):

        for key, value in elements: #calculates the hash of each key

            hashed_value = hash(key)

            index = hashed_value % self.bucket_size # positions the element in the bucket using hash

            self.buckets[index].append((key, value)) #adds a tuple in the bucket

    def get_value(self, input_key):

        hashed_value = hash(input_key)

        index = hashed_value % self.bucket_size

        bucket = self.buckets[index]

        for key, value in bucket:

            if key == input_key:

                return(value)

        return None

    def __str__(self):

        return pprint.pformat(self.buckets) # pformat returns a printable representation of the object

if __name__ == «__main__»:

     capitals = [

        (‘France’, ‘Paris’),

        (‘United States’, ‘Washington D.C.’),

        (‘Italy’, ‘Rome’),

        (‘Canada’, ‘Ottawa’)

    ]

hashtable = Hashtable(capitals)

print(hashtable)

print(f»The capital of Italy is {hashtable.get_value(‘Italy’)}»)

Преимущества:

• Может скрывать ключи в любой форме в целочисленные индексы.
• Чрезвычайно эффективен для больших наборов данных.
• Очень эффективная функция поиска.
• Постоянное количество шагов для каждого поиска и постоянная эффективность добавления или удаления элементов.
• Оптимизирован в Python 3.

Недостатки:

• Хэши должны быть уникальными, преобразование двух ключей в один и тот же хэш вызывает ошибку коллизии.
• Ошибки коллизии требуют полного пересмотра хэш-функции.
• Сложно построить для новичков.

Приложения:

• Используется для больших баз данных, в которых часто ведётся поиск.
• Системы поиска, использующие клавиши ввода.

Общие вопросы собеседования с хеш-таблицей в Python

• Создать хеш-таблицу с нуля (без встроенных функций).
• Формирование слова с помощью хеш-таблицы.
• Найдите два числа, которые в сумме дают «k».
• Реализовать открытую адресацию для обработки коллизий.
• Определите, является ли список циклическим, используя хеш-таблицу.